I started my LeetCode journey on… Well, honestly, I don’t even remember the exact date already. I had several attempts to start solving problems on LeetCode every day, but I never managed to keep it up for more than a few weeks. Until 2022, when I finally managed to establish a daily routine that I have been following for over 1275 days now.
I have learned a lot during this time. Like with everything else, the more you practice, the better you understand the subject. And it turns out that solving problems on LeetCode is not just about algorithms and data structures. Well, they do matter, of course, but there are many other not-so-obvious things that can really help you along the way.
A snapshot of my LeetCode profile
Give yourself time to gain experience
You want to become able to solve hards in 30 minutes? Great! But it won’t happen overnight. You literally have to establish certain neural connections in your brain, and it takes time. The more you practice, the clearer the patterns become to you. And that’s where you start thinking at more abstract levels, which is the key to solving problems faster.
Start with easy problems, cover multiple topics, algorithms, and data structures. Familiarize yourself with the most common concepts. Fortunately, this set is quite finite — it’s not the set of functions continuously differentiable on [0, 1]. I’d say, “pass the first level”. After that, gradually increase the difficulty by moving to mediums, repeat the process, form new connections, and finally advance to hards.
It’s possible. It just takes time.
Programming languages do differ
While many programming languages share similar concepts and are even considered “high-level” and “general-purpose”,
there are still significant differences between them. And it’s not solely about syntax. Take, for example, a standard
collections library. Python offers you a list, a set, and a dict, and that’s pretty much it. C++, on the other
hand, is much richer: it has vector, array, unordered_map, map (“sorted” map, as you may guess; based on
Red-Black or other kinds of trees), unordered_set, set, priority_queue, and many more. Of course, Python also
has all of these, but the way you work with them is different — for priority queues, for instance, you have to use the heapq module together with a list; for sorted sets, you have to use SortedSet from the sortedcontainers
module, etc.
The difference becomes even more pronounced when you start looking at more advanced features like modular arithmetic.
Compare the following:
# Python
>>> -12 % 5
3
// C++
cout << -12 % 5 << endl; // -2
In C++ you also have to be careful with integer overflows:
# Python
>>> 1 << 32
4294967296
// C++
cout << (1 << 32) << endl;
/*
Runtime Error: UndefinedBehaviorSanitizer: undefined-behavior :
shift exponent 32 is too large for 32-bit type 'int'
*/
And understand how exactly parameters are passed to functions:
# Python
def f(c: list) -> list:
c.append(1)
return c
c = []
import time
s = time.perf_counter()
for _ in range(5000):
c = f(c)
print(time.perf_counter() - s) # 0.00032
// C++
vector<int> f(vector<int> c) {
c.push_back(1);
return c;
}
int main() {
vector<int> c;
auto start = chrono::high_resolution_clock::now();
for (int i = 0; i < 5000; ++i) {
c = f(c);
}
auto end = chrono::high_resolution_clock::now();
cout << chrono::duration_cast<chrono::microseconds>(end - start).count() / 1000000.0 << endl; // 0.042879
}
Notice the huge difference in performance. In Python, the function f modifies the list c in place, while in C++ it creates a new copy of the vector every time you call f. So the complexity of the C++ code is actually \(O(n^2)\), while in Python it is \(O(n)\).
Here’s a “fix” for the C++ code:
// C++
vector<int>& f(vector<int>& c) {
c.push_back(1);
return c;
}
// now the time is 0.00018
Learning your language’s peculiarities is an essential part here.
Learn your language’s collections framework
Data structures in general and collections in particular are the most important part of your arsenal. So learning them is crucial. You should know what you have available, how to use them, what their time and memory complexities are, and what their API is. Fortunately, the set of collections is rather small (arrays, sets, maps, queues, stacks, heaps, linked lists, sorted variants of the previous ones, and a couple more), and most languages have a standard library that provides pretty much all of them. Familiarize yourself with the collections framework of your language, and don’t spend too much time (or brain effort) on remembering how to create a max-heap in Python or how to create a sorted set with a custom comparator in C++.
Constants in time & memory complexities do matter
That’s one of my favorite parts!
Pretty much everyone (every book, every course, every blog post) tells you that time and memory complexities are a really important part, and you should learn this \(O\) notation and understand what it means and how to use it. First of all, that’s true. And you have to learn it. But there is one more thing that is often overlooked: this notation (more precisely, when someone makes calculations using this notation) usually omits constants in final complexities. They tell you — “we’re interested in the asymptotic behavior, how the complexity grows with the input size, and not the exact number of operations”. Or even “these two algorithms both have \(O(n)\) complexity, so they’re equivalent in memory/execution time”. And this one — it’s not true.
Why does it happen? Constants in time and memory complexities can show you what exactly is going on under the hood.
Let’s consider the following problem:
Given an array of integers from 1 to 1000 (the length of the array is \(10^5\)), find the most frequent number. If there are multiple such numbers, return the smallest one.
To solve this problem we need to find counts for each number, then find the largest count, and pick the smallest number
among those that have this count. But how do we find the counts? In C++ we can use an unordered_map to store the
counts. What is unordered_map? It’s a hash table (a hash map), which means that it has an average time complexity of
\(O(1)\) for insertions and lookups. Looks great, right? But what happens under the hood?
When we insert a new element into the hash table,
- it calculates the hash of the key,
- finds the bucket where this key should be stored,
- and then inserts the key-value pair into that bucket.
There could also be collisions, which means that two different keys can end up in the same bucket. In this case, the hash table has to handle the collision (usually by chaining or open addressing).
That’s a lot of “internal stuff” happening, and it takes time. So the constant of unordered_map operations is
quite high.
vector, on the other hand, is a dynamic array. It has a much simpler structure: it just stores elements in a
contiguous block of memory. When we edit an element in a vector, it just accesses the memory location of that
element and modifies it. A lot simpler than in unordered_map. And the constant of vector operations is much lower
than that of unordered_map, while the complexity is the same: \(O(1)\) for both.
To use vector in this problem we can leverage the fact that the numbers are in a fixed range (from 1 to 1000).
How does it look in practice?
int main() {
const int n = 100000;
vector<int> arr(n);
for (int i = 0; i < n; ++i) {
arr[i] = rand() % 1000 + 1; // fill with random numbers from 1 to 1000
}
// Using unordered_map
auto start = chrono::high_resolution_clock::now();
unordered_map<int, int> counts_map;
for (int num : arr) {
counts_map[num]++;
}
auto end = chrono::high_resolution_clock::now();
cout << "Time taken using unordered_map: "
<< chrono::duration_cast<chrono::microseconds>(end - start).count() / 1000000.0
<< " seconds" << endl;
// Using vector
start = chrono::high_resolution_clock::now();
vector<int> counts_vector(1001, 0); // 1001 to include 1000
for (int num : arr) {
counts_vector[num]++;
}
end = chrono::high_resolution_clock::now();
cout << "Time taken using vector: "
<< chrono::duration_cast<chrono::microseconds>(end - start).count() / 1000000.0
<< " seconds" << endl;
}
And it outputs something like this:
Time taken using unordered_map: 0.001208 seconds
Time taken using vector: 0.000149 seconds
Almost 10 times faster! While “the complexity” of both solutions is \(O(n)\). Moreover, the memory usage is also lower: unordered_map uses more memory due to its internal structure, while vector just stores the counts in a
contiguous block of memory.
Hacks like this can significantly improve your solution’s performance and avoid TLEs.
In 90% of cases, it’s about the right data structure
A lot of problems on LeetCode are solvable using one and only one data structure that fits the problem perfectly, be it a stack, a queue, a set, a map, or something else. Each data structure has a certain purpose, and provides you with a specific API — what you can do with it, how you can access elements, manipulate them, and so on. It also provides you with complexities for these operations, which is useful when assessing the performance of your solution.
The choice really depends on what you want to achieve, what information you’d like to know about the data. For example, to find the most frequent number in an array, we’d like to know how many times each number appears in the array. It means that we need to store the counts of each number, and we need a data structure that allows us to do that efficiently. Going through the array, and taking numbers one after another, we want to “put them into corresponding boxes” for which we can instantly get the size. This is a perfect use case for a hash map (or a dictionary, or an unordered map, or whatever you call it in your language).
The thing is, it works the opposite way too: if you have a problem, and you don’t know how to solve it, try going through the list of data structures you know, and see if any of them can help you. Start asking questions like:
Okay, maybe I can use a stack here? Will it help me if I store elements on top of each other, and then pop the last one when I need it? I can compare a new element with the last one in the stack, do some magic and create a sorted stack. Will it help me?
More complicated problems may require more complex data structures, like trees, heaps, graphs, or tries. But the idea remains the same.
Even more complicated problems are solved using a combination of data structures. However, they rarely interoperate with each other, and you usually break the problem into smaller consecutive pieces, each of which can be solved using one and only one data structure. But more about that later.
PS: The same applies to algorithms.
In the other 90% —- it’s about finding the right invariant
An invariant is a condition that holds true at a certain point in your program. It can be a property of the data structure (e.g., that your data structure is sorted, or that it contains unique elements only), or a property of the algorithm (e.g., that at the beginning of each iteration, the algorithm has processed all elements before/after the current one).
It’s easier to approach problems by considering different invariants, and then trying to pick the one that actually holds true.
Suppose we’re solving the next one: 198. House Robber. In this problem, we can’t rob two adjacent houses, while we want to maximize the amount of money we can rob. We’re starting from the first house, and we can either rob it or skip it. If we rob it, we can’t rob the second house, but we can rob the third one. If we skip it, we can move to the second house and repeat the process. So a possible invariant here would be that at each step, we’d like to already know the maximum amount of money we can rob starting from any house after the current one. If it holds true, we can easily build a solution:
money[i] = max(
money[i + 1], // skip the current house, and move to the next one
money[i + 2] + houses[i] // rob the current house and skip the next one
);
The next question is: how do we ensure this invariant? Well, here it only means that we should start from the last house and move backwards to the first one, calculating the maximum amount of money we can rob at each step, since the solution for the very last house is trivial (we can rob it, and that’s it).
Of course, this is plain DP (dynamic programming); and yes, DPs are all about invariants. But not only DPs. Graph algorithms, greedy algorithms, and many other algorithms also rely on invariants.
Start by thinking abstractly, and think “in-reverse”
Solve the problem “on a high level” first. Suppose that you can do certain things, you will figure out the real implementation later, now just think about them as building blocks. Break the problem into smaller steps (that later can be implemented as functions).
These building blocks are your arsenal, your higher-level tools. The more tools you know, the faster you’ll be able to solve problems. These tools could be anything: an algorithm, a smaller problem that you have seen before, an operation over a data structure, a mathematical trick, or whatever.
The second part, “think in reverse”, means that it’s usually easier to think about the result you want to achieve first, and then move backwards to the initial state. The all-time question here is “how can I get it?” — what are the steps to get the data I need?
Consider the same problem about finding the smallest most frequent number in an array:
So, I need to find the smallest most frequent number in an array. How can I get it? I may need two things here: the count of each element, and the highest frequency. The latter one is easy to get if I have the counts. So, how do I get the counts? I can use a hash map — I’ll iterate over the array, and for each element, I’ll increment the count in the hash map, starting from 0. Then I can find the maximum count, obviously. Then I can iterate over the elements again, and whenever I see an element with the maximum count (that I just obtained in the second step), I can update my answer if it’s smaller than the current result. Ah, I also have to initialize my answer somehow… Okay, I’ll do that — either with a very large number, or with the first element in the hash map that has the maximum count. Can I optimize this solution somehow? Oh, I can! I can use a vector of size 1001 instead of a hash map to speed up the whole process! Awesome!
Brainteasers are the only exception to this rule, probably, as they usually require you to find some “Aha!” approach. But it definitely works for most other problems on LeetCode.
Brute-force solutions are also valid solutions
Brute-force solutions are often the first thing that comes to mind when you see a problem. At least, they should be. If you can’t come up with a brute-force solution, then “Houston, we have a problem!” — you probably don’t understand the problem well enough (or the topic it covers). Try reading the problem definition several times, pay attention to terms and constraints, or anything else that is in bold. If you still have no clue — hints or other people’s solutions can really help you here.
However, this section is about the validity of brute-force solutions. They are valid. They just may give you a TLE or MLE. But it depends on the problem constraints, and (in reality) the programming language you use. It is funny to see sometimes, but quadratic brute-force solutions in C++ can pass the tests, while the same solution in Python will give you a TLE.
Other cases, like this one - 2044. Count Number of Maximum Bitwise-OR Subsets — Me personally, I don’t know how to solve it without brute-force (and whether it’s even possible or not). So I just, first, find the maximum bitwise OR — the OR of all elements in the array, and then I iterate over all possible subsets (\(2^n\) cases) and count how many of them have the same OR as the maximum one:
class Solution {
public:
int countMaxOrSubsets(vector<int>& nums) {
int r = 0;
for (int v : nums) r |= v;
return count(0, 0, nums, r);
}
int count(int cur, int i, const vector<int>& nums, int t) {
if (i == nums.size()) return cur == t;
return count(cur, i + 1, nums, t) + count(cur | nums[i], i + 1, nums, t);
}
};
And you know what? It works! It passes all tests, and it’s even better than most other C++ solutions:
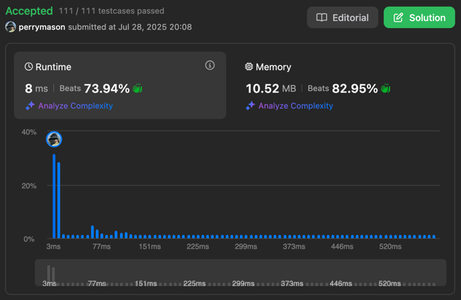
Hint: if the problem constraints say that the input length is at most 20, then you most probably should use a brute-force solution.
Don’t be afraid of failing
It’s OK to not know everything. Moreover, you even shouldn’t know everything. Thousands of people, scientists, and engineers, have been working on algorithms and data structures for decades. This huge amount of knowledge is available to you (thanks to the Internet and, now, to LLMs), and you can use it. You should remember the most crucial ones, like stacks and queues, BFS/DFS, Dijkstra’s algorithm (ideally), but you don’t have to memorize things like “how to implement a segment tree with lazy propagation”.
What is more important here is to become able to implement such algorithms from their descriptions and pseudocode.
For example, this one: 332. Reconstruct Itinerary. Ideally, you should solve it with Eulerian Circuit. It would be great if you can notice that, but it’s ok to not know how exactly to implement it. You can read ideas behind existing approaches, and try to implement it yourself. Check out the internet for descriptions and pseudocodes — there are usually a lot of helpful materials. If it still doesn’t work — ok, you tried, you did your best — check out published solutions, and try to understand how they work. That’s the learning process.
A rule of thumb here is to limit yourself to some time for a problem, and if you can’t solve it in that time, try looking at hints first, then at titles of existing solutions, and finally at the solutions themselves. I usually give myself about 2 hours before looking at hints. The thing is, I do it less and less often now.
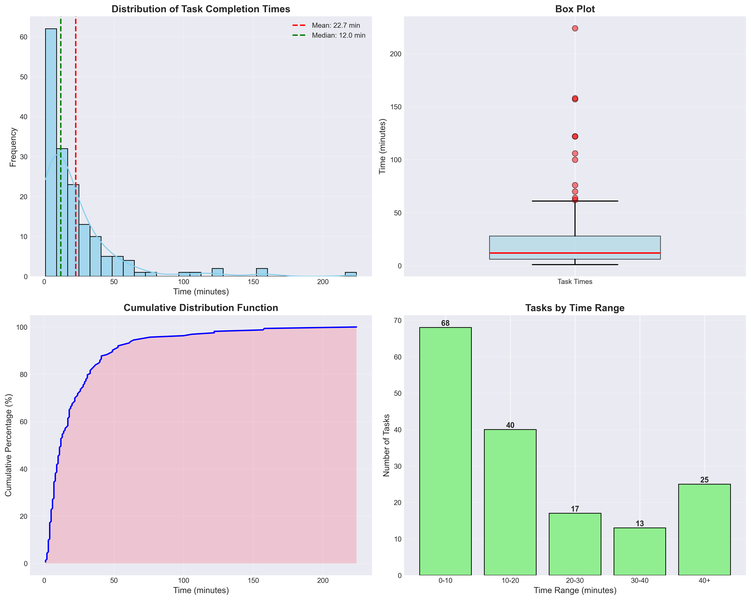
Here are some statistics about time taken to solve problems for the last half a year (not all problems were logged, unfortunately):
Total tasks: 163
Average time per task: 22.68 minutes
Percentiles: 25% = 6.00, 50% = 12.00, 75% = 28.00
Total time spent: 3697.00 minutes (61.62 hours)
Shortest task: 1.00 minute
Longest task: 224.00 minutes
Consistency is key
Just as LeetCode tells you, consistency is the key. Forming new neural connections takes time. And it’s much easier to do it gradually, day by day, than trying to learn everything in a week before the interview and burn out and oversleep the meeting you were preparing for. It also helps you to retain the knowledge you have already gained, as we, humans, tend to forget things we don’t use regularly.
After all
Don’t forget about the trivials:
- estimate the time and memory complexities;
- check corner cases. Think what can go wrong, and which pieces of your solution are the most prone to fail (hint: indexing, nested for loops, etc). Fortunately, LeetCode allows you to add custom test cases (though they restrict it to 8 currently);
- think about an algorithm and data structures before writing the code. It’s easier to rewrite code in your head than in the editor. Think abstractly, establish a hierarchy, break everything into functions, and only then implement it in code;
- proofread what you have written. Use appropriate variable names, pay attention to indexing, fix typos and syntax errors, and so on.
Conclusion
A lot of stuff… And only one question: Why? It’ll take some time to explain, but the short answer is: fun! I just like solving leetcode every day, and I hope these tips will help you to enjoy it too. I’ll cover more about the pros and cons of solving problems on LeetCode every day in the next post.